Slides_Quan201_Topic6_Heteroskedasticity slides

QUAN201 - Introduction to Econometrics¶

datetoday = Dates.datetime.today().strftime("%m/%d/%Y")

Reference: Wooldridge, Chapter 8

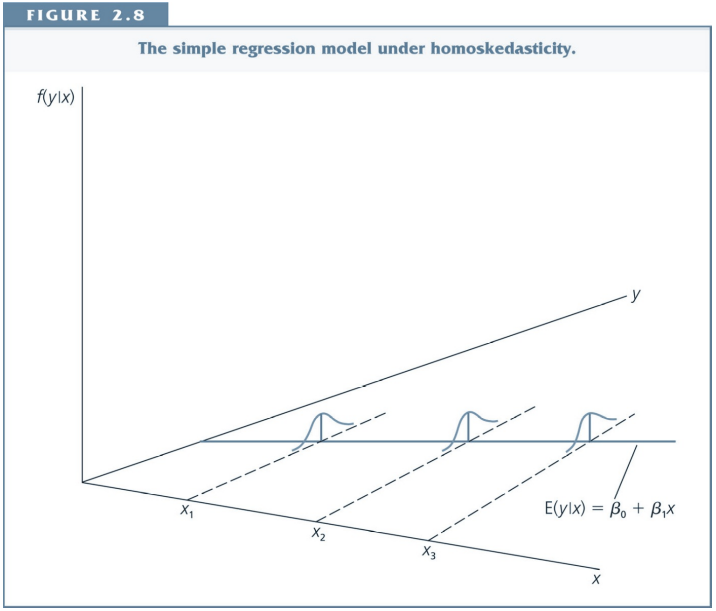
Recall Assumption MLR.5: Homoskedasticity. The error $u$ has the same variance given any value of the explanatory variables: $$ Var(u|x_1,x_2,...,x_k)=\sigma^2 $$
If this is not the case, there is heteroskedasticity.
What does this mean?

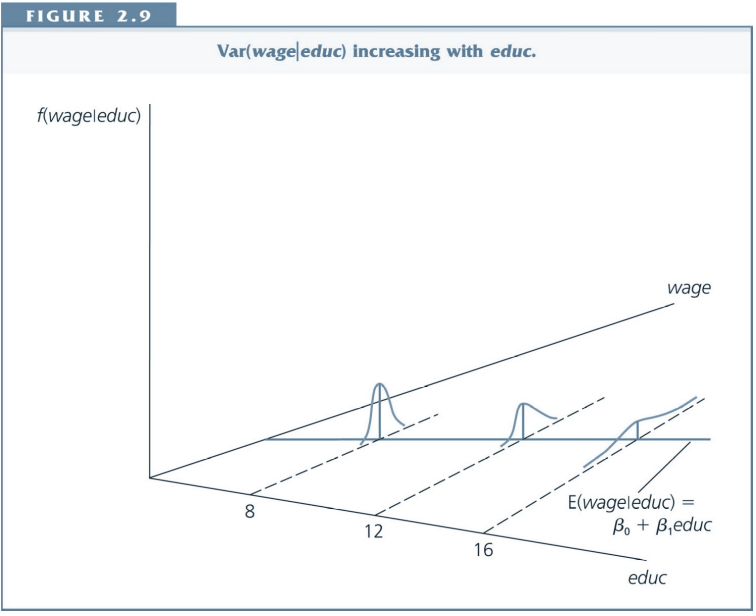
Consider the following model: $$wage=\beta_0+\delta_0 female +u$$
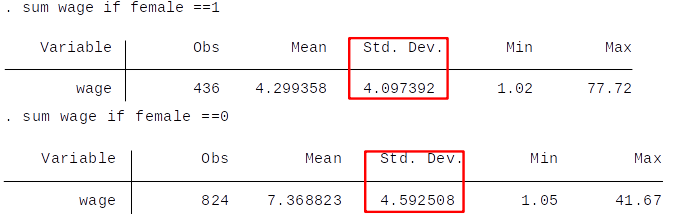
Homoskedasticity means that the variance of the error term $u$ (and in this case the variance of wages) is the same for females and males.
Is this realistic? Discuss.
Let's look at the summary statistics,

Heteroskedasticity leads to incorrect inference-
- t-statistics, F-statistics, confidence intervals and p-values are no longer valid.
OLS is no longer the most efficient estimator (OLS is no longer BLUE), i.e., there might be other estimators like WLS that are more efficient.
Heteroskedasticity does not
- cause bias or inconsistency
- affect the interpretation of $R^2$

Imagine that you estimate the following linear model, $$ y= \beta_0 + \beta_1 x_1 + \beta_2 x_2 + ...+ \beta_k x_k + u $$ where all the other CLM assumptions hold. Most importantly the assumption that $E[u|\textbf{x}]=0$ holds implying that the OLS is unbiased and consistent ($\textbf{x}=<x_1,x_2,...,x_k>$).
The null hypothesis, $$ H_0: \, Var(u|\textbf{x})=E[u^2|\textbf{x}]=\sigma^2$$ says that the error variance is constant, i.e., homoskedastic.
[Note: $Var(u|\textbf{x})=E[u^2|\textbf{x}]$ is not generally true, but here follows from $E[u|\textbf{x}]=0$.]
The idea of the Breusch-Pagan test is to examine whether $u^2$ (the variance of the error) is related to one or more variables: $$ u^2=\delta_0 + \delta_1 x_1 + \delta_2 x_2 +...+\delta_k x_k + \upsilon $$

Then the null hypothesis $ H_0: \, Var(u|\textbf{x})=E[u^2|\textbf{x}]=\sigma^2$ suggests using, $$ H_0: \delta_1 = \delta_2 = ...=\delta_k=0$$
This means that the independent variables are not (linearly) related to the variance of error term $u$.
The main issue is that it is impossible to know the error terms $u$.
How can we obtain estimates for the error term to test this hypothesis? We use the OLS residuals $\hat{u}^2$ as estimates of the error term. The equation then becomes $$ \hat{u}^2 = \delta_0 + \delta_1 x_1 + \delta_2 x_2 +...+\delta_k x_k + \upsilon $$
We can estimate this equation and test $H_0$ with an F-test. If the F-test rejects $H_0$ we have evidence for heteroskedasticity.

Estimate the original model.
Obtain the residuals, and calculate their squares.
Run a regression with the squared residuals as dependent variable and the same explanatory variables as in the original model as independent variables.
Run an F-test of joint significance of all explanatory variables for this regression:
- If the p-value is larger than the critical value: we don’t reject the null hypothesis of homoskedasticity
- If the p-value is smaller than the critical value: we have evidence for heteroskedasticity.

We can use heteroskedasticity robust standard errors, t-statistics, f-statistics, confidence intervals and p-values.
These lead to valid inference in the presence of heteroskedasticiy of unknown form.

$$ \widehat{Var(\beta_j)} = \frac{\sum_{i=1}^n \hat{r}_{ij}^2 \hat{u}_{ij}^2 }{SSR_j^2} $$ where,

$\hat{r}_{ij}$ is the residual for person $i$ from a regression of $x_j$ on all the other independent variables.
$SSR_j$ is the sum of squared residuals from same regression of $x_j$ on all the other independent variables.

Heteroskedasticity robust inference is very easy to implement and now standard in applied economics.
- In Stata, simply add ",robust" to the OLS command.
Note that the robust test statistics are only asymptotically valid. That means that in small samples, the normal test statistics are preferred in the absence of heteroskedasticity.

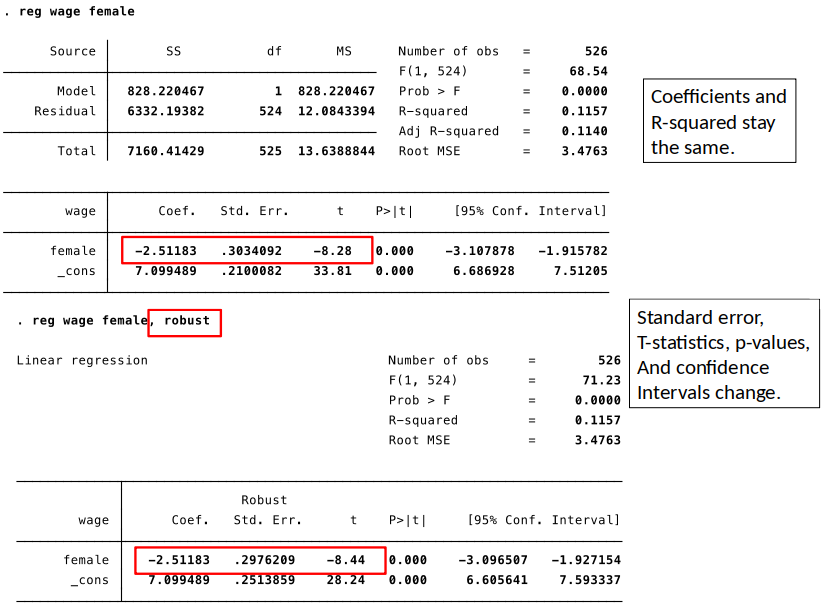
Is this heteroskedasticity? Or homoskedasticy?

Could Breusch-Pagan test answer this?

The White test for heteroskedasticiy has the same setup as the Breusch-Pagan test but adds some flexibility by also testing whether the squared residulas are related to the squared terms and cross products of the independent variables.
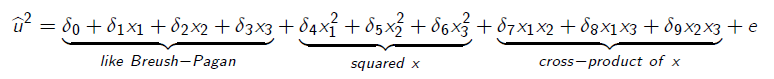
In the rare case that we know the variance of the error term we can estimate the regression using Weighted Least Squares (WLS). Under heteroskedasticity WLS is more efficient than OLS.